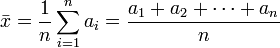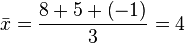MEDIA
la media aritmética (también llamada promedio o simplemente media) de un conjunto finito de números es igual a la suma de todos sus valores dividida entre el número de sumandos. Cuando el conjunto es una muestra aleatoria recibe el nombre de media muestral siendo uno de los principales estadísticos muestrales.
EJEMPLO:
Dados los
n números
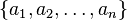, la media aritmética se define simplemente como:
Por ejemplo, la media aritmética de 8, 5 y -1 es igual a:
Se utiliza la letra
X con una barra horizontal sobre el símbolo para representar la media de una muestra (
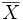), mientras que la letra µ (
mi) se usa para la media aritmética de una población, es decir, el
valor esperado de una variable.
Varianza y desviación estándar
La desviación sólo significa qué tan lejos de lo normal
Desviación estándar
La desviación estándar (σ) mide cuánto se separan los datos.
La fórmula es fácil: es la raíz cuadrada de la varianza. Así que, "¿qué es la varianza?"
Varianza
la varianza (que es el cuadrado de la desviación estándar: σ
2) se define así:
Es la media de las diferencias con la media elevadas al cuadrado.
En otras palabras, sigue estos pasos:
1. Calcula la
media (el promedio de los números)
2. Ahora, por cada número resta la media y eleva el resultado al cuadrado (la diferencia elevada al cuadrado).
3. Ahora calcula la media de esas diferencias al cuadrado. (
¿Por qué al cuadrado?)
Ejemplo
Tú y tus amigos habéis medido las alturas de vuestros perros (en milímetros):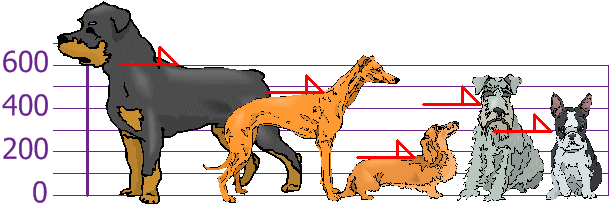
Las alturas (de los hombros) son: 600mm, 470mm, 170mm, 430mm y 300mm.
Calcula la media, la varianza y la desviación estándar.
Respuesta:
| Media = | 600 + 470 + 170 + 430 + 300 | = | 1970 | = 394 |
| |
5 | 5 |
así que la altura media es 394 mm. Vamos a dibujar esto en el gráfico:
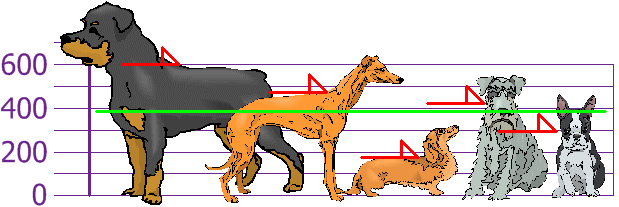
Ahora calculamos la diferencia de cada altura con la media:
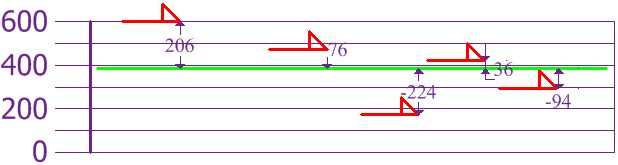
Para calcular la varianza, toma cada diferencia, elévala al cuadrado, y haz la media:
| Varianza: σ2 = | 2062 + 762 + (-224)2 + 362 + (-94)2 | = | 108,520 | = 21,704 |
| |
5 | 5 |
Así que la varianza es 21,704.
Y la desviación estándar es la raíz de la varianza, así que:
Desviación estándar: σ = √21,704 = 147
y lo bueno de la desviación estándar es que es útil: ahora veremos qué alturas están a distancia menos de la desviación estándar (147mm) de la media:
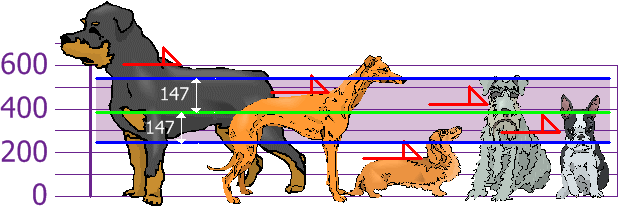
Así que usando la desviación estándar tenemos una manera "estándar" de saber qué es normal, o extra grande o extra pequeño.
Los Rottweilers son perros grandes. Y los Dachsunds son un poco menudos... ¡pero que no se enteren!
